This Cleaning Memo, entitled “Process Capability Index for Cleaning Validation”, discusses what a process capability index is, how it is typically utilized, and how it has been promoted for cleaning validation. It includes a discussion of the limitations and value of process capability index considerations for cleaning validation in the pharmaceutical world.
Process capability is generally defined as something like “a measure of the consistency of a process based on a statistical evaluation, focusing on the mean and standard deviation, of a sufficient number of data point reflective of the quality of the process”. Now this definition (which is mine) is in some sense circular because it defines “process capability” using the phrase “consistency of a process”. However, I suspect you know that I am talking about. It can be formally evaluated by use of a Process Capability Index (commonly referred to as “Cpk”).
Here is what is done in a process capability evaluation. It is typically used for processes where there is a defined target value for a measured characteristic. In many processes there are both an upper specification level (USL) and a lower specification level (LSL). Doing a process capability evaluation on the amount of active in a tablet would be an example where there is both an USL and a LSL. However, for cleaning processes where we are specifically looking for residues of chemical species (such as actives or cleaning agents) on surfaces in cleaned equipment, there is generally only an USL (what is generally referred to as the “limit” based on a carryover calculation). So, this type of capability index is generally called a “Cpu”, since a comparisons is only made to the USL. So, how is the Cpu calculated? It is generally done where there are sufficient data points (usually a minimum of around fifty). The average (the “mean”) and then a standard deviation (SD) are calculated for those data, with the Cpu being calculated as follows:
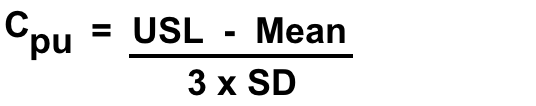
It should be obvious that the larger the difference between the USL and Mean, the higher the Cpu value will be. Also, the lower the SD, the higher the Cpu value will be. So, high Cpu values are desirable. How high should the Cpu be? Generally, values like 1.50 or higher are preferred, because that means that the data will be within the USL with a reasonable probability.
I will illustrate this for swab data for a cleaning process. Suppose I have fifty data points for a given cleaning process on a given drug product. Does it make sense to calculate a Cpu for that data? Well my answer is that it depends on what those fifty data points are. If I have performed the cleaning process on each of fifty batches of the same product and have one data point on the same equipment location for each of the fifty batches, then it is certainly possible to meaningfully evaluate the Cpu for the data for that specific location. However, I should also do a Cpu for data for each of the other specific sample locations for that cleaning process. Some might want to combine together the measured values for all the swab data locations; in that way I can more easily achieve my 50 data points in a fewer number of consecutive batches. I guess it is possible to do that, but is it really meaningful or am I just playing games with the data?
The issue is what constitutes the “same population” for statistical evaluation purposes. Certainly in a cleaning validation situation the individual swab locations selected for sampling (such as a sidewall, a dome, an agitator shaft, an agitator bade, and the like) are not the same population, nor do I expect to get the same data in each situation for a specific product that is cleaned. An exception to expecting the same data is where the data is “non-detected” (that is, less than the LOD). However, as long as the LOD is well below the limit (the USL), what is the point of doing a calculation of Cpu (other than “busy work”)?
For comparison, it is relatively easy to obtain fifty data points for process validation where my measured output is the level of active in a tablet (but still I am still going to do it on samples at different times within a batch and with samples from multiple consecutive batches). But the point is that in a process validation situation the measurements are from the same population. In cleaning validation where there are multiple swab locations for the equipment, those swab locations are not the same, which is the rationale behind selecting worst-case swab locations. Some swab locations (as compared to other locations) are more likely to have higher levels of measured residue.
So, let’s take a look at some examples where all the swab data (that is, from all locations in the equipment) is combined to determine a Cpu for cleaning for a specific product and cleaning process.
Example #1:
In this example, I have fifty swab results. Of those, twenty are 1.0 mcg/swab, ten are 2.0 mcg/swab, and twenty are 3.0 mcg/swab. My cleaning validation limit (from a carryover equation) is 10 mcg/swab (this is the USL). The calculated mean is 2.0 mcg/swab, and the calculated SD is 0.90 mcg/swab. Using the equation previously given, the Cpk is 3.0. Both a practical assessment of the data and the Cpu value suggest that I should be happy with the data.
Example #2:
In this example, I also have fifty swab results. Of those, forty seven are 1.0 mcg/swab and three are 5.0 mcg/swab. My cleaning validation limit (calculated from a carryover equation) is 10 mcg/swab. The calculated mean is 1.2 mcg/swab, and the calculated SD is 0.90 mcg/swab. Using the equation previously given, the Cpu is 3.0. Compared to Example #1, does the lower mean and the same Cpu mean I should be happy with these results? While it does mean I meet my acceptance criterion, the three higher data values should be of some concern. I should consider evaluating the sampling locations of those three higher results to see if there is anything indicating that any of those locations suggests a need to improve my cleaning process. For example, if all three higher results are from the same sampled location (perhaps on cleaning of three different drug product batches), then some kind of corrective or preventive action might be taken (either to lower the measured values for those locations or to prevent those measured values from going much higher).
Example #3:
In this example, I also have fifty swab results. Of those, forty nine are 1.0 mcg/swab and one is 8.0 mcg/swab. My cleaning validation limit (from a carryover equation) is 10 mcg/swab. The calculated mean is 1.1 mcg/swab, the calculated SD is 1.0 mcg/swab, and the Cpu is 3.0. Compared to Example #2, does the lower mean and the same Cpu mean I should be happy with these results? While it does mean I meet my acceptance criterion, that one higher data value of 8.0 mcg/swab should raise significant concerns. I should probably pay more attention to that one sampling location (for example, if this is data from multiple batches, what were the results for that sampling location for other batches). Collecting more data on additional batches may help alleviate concerns if subsequent data is all closer to 1.0 mcg/swab, or that additional data may point to a significant issue with that sampling location. This would be another case where a Cpu determination is interesting, but is probably not critical for establishing the consistency of the data (remembering that the critical aspect of consistency for cleaning validation purposes when different sampled locations are considered is that the data be consistently below the calculated limit, and preferably be consistently well below the calculated limit).
Example #4:
In this fourth example, I also have fifty swab results. Of those, ten are 1.0 mcg/swab, ten are 2.0 mcg/swab, ten are 3.0 mcg/swab, ten are 4.0 mcg/swab, and ten are 5.0 mcg/swab. The cleaning validation limit (from a carryover equation) is 10 mcg/swab. The calculated mean is 3.0 mcg/swab, the calculated SD is 1.4 mcg/swab, and the Cpu is 1.6. While this Cpk is much lower than in the other examples, it is still what is generally considered a “good” Cpu value. However, despite that Cpu value I would probably want to improve my cleaning, not because of any concern with the consistency of the process, but rather because of a concern about the robustness of the cleaning process. Other things being equal, I generally teach that the goal in the design of a cleaning process should be to have measured values that are in the range of 20% (or below) of the calculated limits, thus clearly demonstrating the robustness of the cleaning process.
Example #5:
In this final example, I also have fifty swab results. Of those, forty two are 8.0 mcg/swab, four are 7.0 mcg/swab, and four are 9.0 mcg/swab. The cleaning validation limit (from a carryover equation) is 10 mcg/swab. The calculated mean is 8.0 mcg/swab, the calculated SD is 0.4 mcg/swab, and the Cpu is 1.6. That Cpu is the same as the Cpu for Example #4. Clearly in this example, while the Cpu may be a reliable indicator of statistical control, this type of data is generally not data that most companies would want to have for a robust validated cleaning process.
It should be noted in the examples presented that it is assumed the data is from different sampling locations in the same equipment for cleaning of a given product. For me, this calls into question the applicability of doing statistical evaluations such as Cpu for cleaning validation. While this doesn’t hurt (except perhaps to suggest that one does not fully know the limitations of statistics), it certainly can be done. And particularly if your company requires a Cpu calculation, it is probably simpler to just do it rather than try to convince the company otherwise. In any case, consider the advice once given by my favorite statistician (Dr. Lynn Torbeck) who said something like “First determine if differences in the data are practically significant before you try to look for statistical significance” (not his exact words, but my summary of the principle).
In subsequent Cleaning Memos (in August and September), I will discuss alternatives to a process capability index as a means of evaluating the “health” of data in a cleaning validation program. Those alternatives include use of appropriate histograms and appropriate tending charts.
Finally for clarification I should state that I am not a statistician (you probably had already figured that out). Furthermore, the examples presented were artificially designed to illustrate my argument; those examples are not actual client data.
Copyright © 2022 by Cleaning Validation Technologies