This is part of a clarification on a topic I have written about in the past (See the July 2001 Cleaning Memo) and where I have subsequently expanded on in my training seminars and webinars, but have not updated in Cleaning Memos on my website. So this is an opportunity to share that information with those of you who have not attended my seminars or webinars.
Product grouping (also called matrixing, family approach, or bracketing) involves selecting a representative product among a group, performing a cleaning validation protocol on that representative product, and applying the validation result to all products in the group. Products in a group are usually the same type of product (liquid, solid, semisolid) manufactured on the same or equivalent equipment and cleaned by the same cleaning process. Ordinarily, the representative product is the worst-case product. I generally identify the worst-case product as the product that is “most difficult to clean”. That is, if I can clean the “most-difficult-to-clean product” acceptably, the other products in the group should also be cleaned acceptably.
Part of the criteria for determining that the worst-case product is cleaned acceptably is setting residue limits for that worst-case product. That is, let’s assume I have products A, B, C, and D in a group. I determine (by whatever criteria) that A is the worst case. What limits do I establish in my protocol when I perform my protocol on A? Do I calculate my residue limit for A based on carryover calculations utilizing each of the other products (B, C, and D) as the next product, and then select the lowest of those possible limits as the limit for my protocol? The issue in such an approach is that it may be appropriate in some situations, but not in other situations. Here are several examples to illustrate the issue.
Example 1
Suppose that A is the worst case product (most difficult to clean). Here are my calculated limits in µg/cm2 for the cleaning for each of A, B, C, and D. In each case, the lowest limit for each cleaned product is italicized.
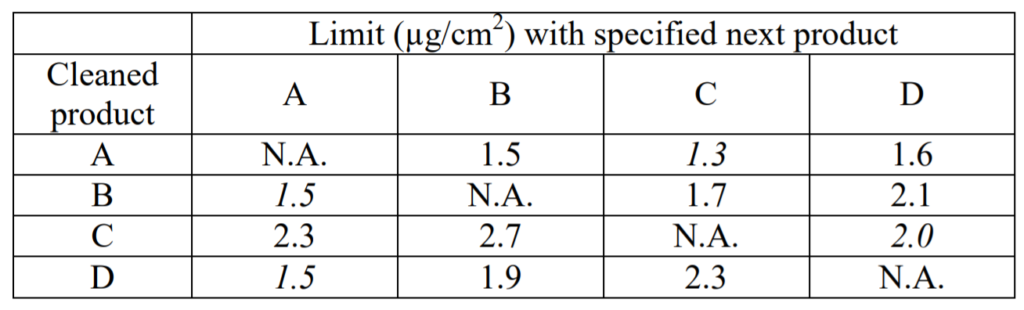
In this situation, if I cleaned A down to a limit of 1.3, then the other three products (which are easier to clean) should also be cleaned down to a limit of 1.3, which is below the lowest limit for those other three products. In this example, cleaning of A down to its limit of 1.3 provide assurance that the other three products are effectively cleaned at their calculated limits.
Example 2
In this example, we will still suppose that A is the worst-case product (most difficult to clean), but the calculated residue limits are different, as given in the table immediately below.
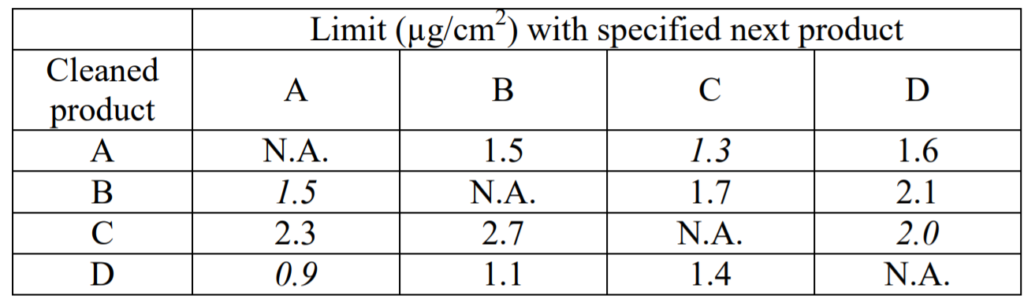
In this situation, if I cleaned A down to a limit of 1.3, then products B and C (which are easier to clean) should also be cleaned down to a limit of 1.3, which is below the lowest limit for each of those two products. However, applying that data to Product D is a problem. Product D is easier to clean than A, so it should be cleaned down to a limit of 1.3; however, I need to have it cleaned down to a level of 0.9, significantly lower than 1.3. Therefore, in this situation, cleaning A down to its calculated limit (based on what is the worst case next product) does not provide assurance that I have covered the situation of cleaning D down to its calculated limit.
In the early days of cleaning validation, the attempt to resolve this dilemma in a grouping approach was to perform one protocol on the worst-case (most difficult to clean) product and a separate protocol on the “most toxic” product. What was meant by “most toxic” product is the product with the lowest limit. So in the case of Example 2, I would perform one protocol on A at its limit of 1.3 and one protocol on D at its limit of 0.9. With these two protocols for Example 2, I have effectively shown that I can cover the cleaning validation of all four products by this strategy. However, while this strategy works well in the example given, let’s take a look at another example where that approach is problematic.
Example 3
In this example, we will still suppose that A is the worst case product (most difficult to clean), but the calculated limits are different, as given in the table below.
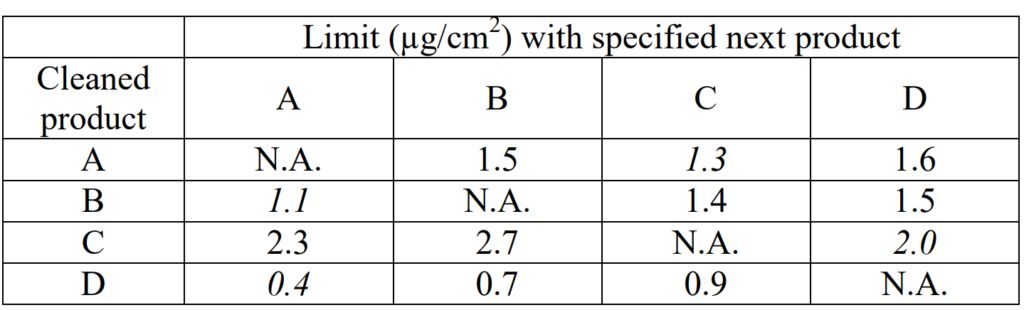
For this example, let’s suppose the order of difficulty of cleaning is as follows:
Most difficult: A
Second most difficult: B
Third most difficult: C
Fourth most difficult: D
For clarification, this means that D is the easiest product to clean.
Let’s say in this example I tried the approach of one protocol for the “most-difficult-to-clean” product and one protocol for the “most toxic” product. Would this cover all four products? In this example, if I cleaned A down to a limit of 1.3, then product B (easier to clean) should also be cleaned down to a limit of 1.3; however, I need to have it cleaned down to a lower limit of 1.1. Can I then look to have B covered by a separate protocol for the “most toxic” product, which is D? If I can clean D to a limit of 0.4, what does it mean for B? The answer is that I can’t come to a logical conclusion because D is easier to clean than B. In other words, just because D can be cleaned to a limit of 0.4, I can’t say anything about what that means for B, even though the limit for B is higher. For those of you who are wondering about C, it is easier to clean than A and has a higher limit; therefore, cleaning of A at its limit is adequate to establish that C is effectively cleaned.
One approach for all examples
The way to cover all of these examples given with one protocol is to perform the cleaning process on the most-difficult-to-clean product using the lowest limit of any product in the group. In Example 1, this would mean a protocol with product A at a limit of 1.3. In Example 2, this would mean a protocol with product A at a limit of 0.9. In Example 3, this would mean a protocol with product A at a limit of 0.4. The beauty of this approach is having one approach that covers all situations.
Some may object that by including the toxicity or limit factor in the selection of the “worst-case” product, they have adequately addressed the issue of lower limits. That is, they may have used a “point system” which includes a “toxicity” factor (such as by a PDE value or by a limit calculation) as well as factors such as solubility of the active. While that may sound plausible, it still doesn’t adequately and logically cover all situations. It is not unlike the old grouping approach of “most-difficult-to-clean” and “most toxic”, where it is possible to have some products “fall through the cracks”. I should make it clear that my preference is not to use a toxicity factor in determining which product is “most-difficult-to-clean”. Toxicity may be a risk factor, but toxicity per se does not make something more difficult to clean. As a risk factor, toxicity is addressed by selecting the lowest limit of any product in the group. The only exception to this preference is if I have two products which are equally difficult to clean, and one is highly hazardous and one is not highly hazardous. In that situation, I would prefer to use the highly hazardous product as the worst-case product in a grouping approach.
Others may object that it may not be possible to analyze the most-difficult-to-clean product at the lowest limit of any product in the group. That is a valid concern. If a better analytical technique cannot be found, it may be necessary to divide the products into two (or more) groups to cover all situations. The approach in this situation (in terms of forming the two groups) will depend on the number of products, the relationship between difficulty of cleaning among products, the calculated limits, and the available analytical methods.
The objective of this Cleaning Memo is to present valid concerns for selecting products and limits for use in product grouping approaches for cleaning validation